दज़ानिबेकोव प्रभाव
जिज्ञासु के लिए भौतिकी के क्षेत्र से आज कुछ: द Dzhanibekov प्रभाव, जिसे टेनिस रैकेट प्रमेय के रूप में भी जाना जाता है, जड़ता के तीन अलग-अलग क्षणों के साथ निकायों को घुमाने की एक अस्थिरता की व्याख्या करता है। जड़ता का क्षण शरीर के प्रतिरोध को उसके घूर्णी आंदोलन में परिवर्तन को इंगित करता है। यह रोटेशन की विशेष धुरी और ज्यामिति पर निर्भर करता है। शास्त्रीय हैमिल्टनियन प्रणालियों की गतिशीलता को समझना अभी भी एक महत्वपूर्ण लक्ष्य है अनुप्रयोगों की एक भीड़ के साथ जो उनके गणितीय विवरण से बहुत आगे जाते हैं। स्वतंत्रता की कुछ डिग्री के साथ पूर्णांक प्रणालियों के मामले में, एक कुशल दृष्टिकोण यांत्रिक प्रणाली के गतिशील गुणों की विशेषता के लिए एक ज्यामितीय विश्लेषण पर आधारित है। इस तरह की ज्यामितीय घटनाएं आम तौर पर कुछ प्रभावों की प्रबलता की उत्पत्ति होती हैं जिन्हें प्रयोगात्मक रूप से देखा जा सकता है। उनमें से एक तथाकथित है। Dzhanibekov प्रभाव या टेनिस रैकेट प्रभाव भी कहा जाता है।
आईएसएस के भारहीनता में जानिबेकोव प्रभाव
घटना का एक उत्कृष्ट और विस्तृत सैद्धांतिक व्युत्पत्ति यहाँ पाया जा सकता है (https://arxiv.org/pdf/1606.08237.pdf)। हम यहां एक ऐसे व्यक्ति के साथ काम कर रहे हैं जो थोड़ा मोटा है, लेकिन जो फिर भी इस घटना की व्याख्या करता है। दुर्भाग्य से, कठोर निकायों की गतिशीलता का कुछ पूर्व ज्ञान यहां आवश्यक है:
जड़ता I1 और I2 और I3 के क्षणों के साथ मैट्रिक्स की जड़ता (विकर्ण) पर विचार करें जैसे कि I1 सबसे छोटा है और I3 सबसे बड़ा है। अब जड़ता I3 के मुख्य क्षण की धुरी के चारों ओर आंदोलन पर विचार करें। कोणीय वेग वेक्टर है:
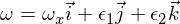
जहाँ एप्सिलॉन अन्य दो मुख्य अक्षों में छोटे छिद्र होते हैं। यदि आप अब इसे यूलर समीकरणों में सम्मिलित करते हैं, तो आपको यह मिलता है:
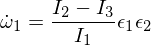
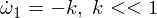
अब हम दूसरे यूलर समीकरण को अलग करते हैं:
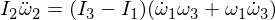
हमारी अभिव्यक्ति में ओमेगा 1 और ओमेगा 3 का प्रतिस्थापन, और चूंकि एप्सिलॉन को गुणा करना उन्हें छोटा करने के लिए पर्याप्त बनाता है,
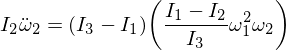
यह हमें प्रपत्र के ओमेगा 2 के लिए एक अंतर समीकरण देता है:
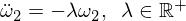
मूल समाधान है:
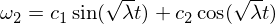
इसलिए हम जानते हैं कि ओमेगा -1 अक्ष में घूर्णी विकार स्थिर है और समय-समय पर आंदोलनों, या कठोर शरीर आंदोलन की शब्दावली में, कि यह एक पूर्वसूचक बनाता है। ओमेगा 3 विकार ऊपर दिए गए एक समान तर्क का अनुसरण करता है, और मैं इसे आपके माध्यम से काम करने के लिए एक अभ्यास के रूप में छोड़ दूँगा। मध्यवर्ती अक्ष के लिए हमारे पास है:
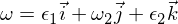
यूलर समीकरणों में सम्मिलित:
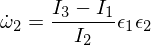
तीसरे यूलर समीकरण को विभेदित करता है:
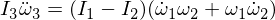
आइए हमारे व्युत्पन्न भावों को बदलें:
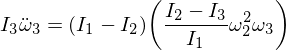
अब निम्नलिखित अंतर समीकरण को फिर से व्यवस्थित करें और प्राप्त करें:
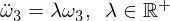
ध्यान दें कि गुणांक अब सकारात्मक है, जो इसलिए घातीय समाधान की ओर जाता है:
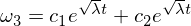
इस समाधान से पता चलता है कि ओमेगा 3 ओमेगा 2 की गड़बड़ी के साथ मध्यवर्ती अक्ष के साथ अस्थिर है!
क्या बेडियेट दास था?
अब हम वह सब कुछ जोड़ सकते हैं जो हमने प्राप्त किया है और प्रमेय को समझना सीख लिया है। सीधे शब्दों में कहें: यदि मध्यवर्ती अक्ष के साथ रोटेशन परेशान है, तो घातीय समाधान परिणामों के साथ एक अंतर समीकरण। यह अन्य दो अक्षों में देखे गए सटीक आंदोलन के विपरीत, एक अस्थिर आंदोलन की ओर जाता है। यह परिणाम काफी आश्चर्यजनक है। इस तरह के प्रमेय के लिए कोई सहज समर्थन नहीं है क्योंकि हम कल्पना नहीं कर सकते कि जड़ता के मध्यवर्ती क्षण का परिणाम अस्थिर रोटेशन क्यों होगा। ऐसा लगता है कि यह प्रकृति में विशुद्ध रूप से गणितीय है।